
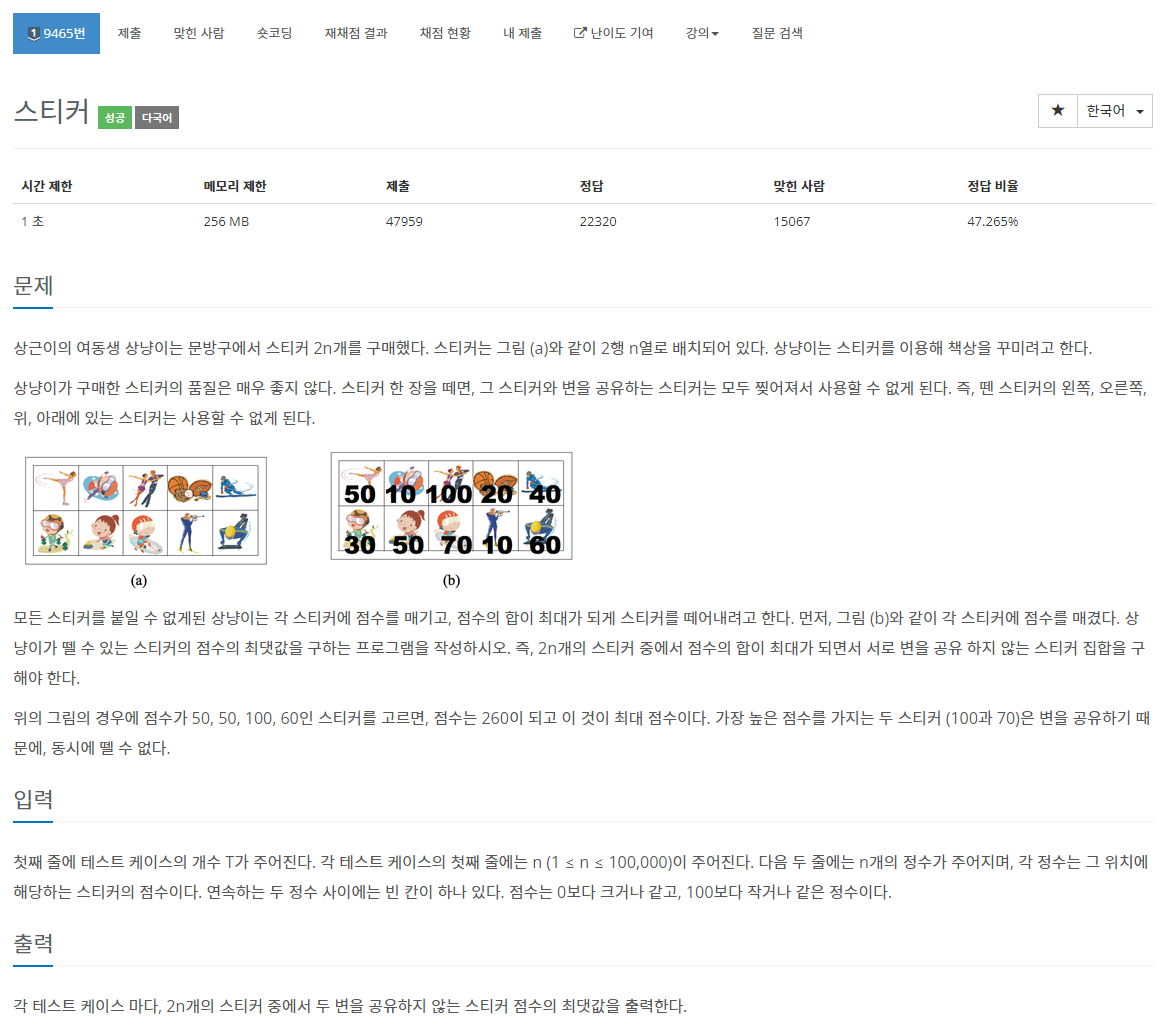
# 답
for _ in range(int(input())):
n = int(input())
sticker = [list(map(int, input().split())) for _ in range(2)]
dp = [[0] * n for _ in range(2)]
for i in range(2):
dp[i][0] = sticker[i][0]
if n > 1:
dp[i][1] = sticker[i ^ 1][0] + sticker[i][1]
for j in range(2, n):
for i in range(2):
dp[i][j] = max(dp[i ^ 1][j - 2], dp[i ^ 1][j - 1]) + sticker[i][j]
print(max(dp[0][n - 1], dp[1][n - 1]))
# 분석 1
dp 테이블은 2 * n 크기의 배열로 만들고 다음과 같은 규칙으로 채워나갑니다.
" 왼쪽에서부터 스티커를 선택해나갈 때, 각 칸을 마지막으로 골랐을 경우의 점수 최댓값을 기입할 것 "
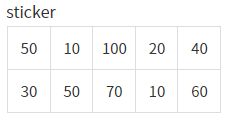
문제에 나왔던 예시를 가지고 설명해보겠습니다.
스티커의 점수는 왼쪽과 같이 입력으로 제시되었습니다.
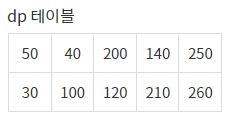
dp 테이블을 앞서 말했던 규칙에 따라 일일이 작성해보세요.
그럼 왼쪽과 같이 작성됩니다.
dp 테이블을 만들면서 규칙을 발견하셨나요?

위 그림에서 A를 제일 마지막 스티커로로 선택할 경우,
A 말고 선택될 수 있는 스티커는 F 또는 D 밖에 없습니다.
(* E는 D가 선택될 경우 자동으로 같이 선택되는 것이나 다름없습니다.)

반대로 B를 제일 마지막 스티커로 선택할 경우,
B 말고 선택될 수 있는 스티커는 E 또는 C 밖에 없습니다.
(* 마찬가지로 F는 C가 선택될 경우 자동으로 같이 선택된다고 간주합니다.)
그러니 dp 테이블을 작성할 때,
0행 n열의 값은 1행 n - 1열, 1행 n - 2열의 값 중 큰 값을 취하면 되고,
1행 n열의 값은 0행 n - 1열, 0행 n - 2열의 값 중 큰 값을 취하면 됩니다.
# 분석 2
답안 코드를 보시면 i ^ 1 이라는 표현이 있습니다.
이 표현을 처음 접하시는 분들도 계실텐데요.
for i in range(2):
dp[i][j] = max(dp[i ^ 1][j - 2], dp[i ^ 1][j - 1]) + sticker[i][j]결론부터 말하자면 ^는 비트연산자 XOR을 수행합니다.
XOR은 1이 홀수개이면 1을 반환하고 짝수개이면 0을 반환하는 연산자입니다.
즉 1 XOR 1 == 0이고, 1 XOR 0 == 1 입니다.
현재 우리는 i == 0일 때는 1의 값이 필요하고, i == 1일 때는 0 값이 필요한 상황입니다.
따라서 i ^ 1 라고 쓰면 i 값의 정반대가 되는 값을 취할 수 있게 되는 것입니다.
'Algorithm > BaekJoon' 카테고리의 다른 글
| (파이썬) 백준 3053번 "택시 기하학" (0) | 2022.05.11 |
|---|---|
| (파이썬) 백준 2343번 "기타 레슨" (0) | 2022.04.29 |
| (파이썬) 백준 1463번 "1로 만들기" (0) | 2022.04.25 |
| (파이썬) 백준 2805번 "나무 자르기" (0) | 2022.04.24 |
| (파이썬) 백준 9663번 "N-Queen" (0) | 2022.04.24 |
