
그래프
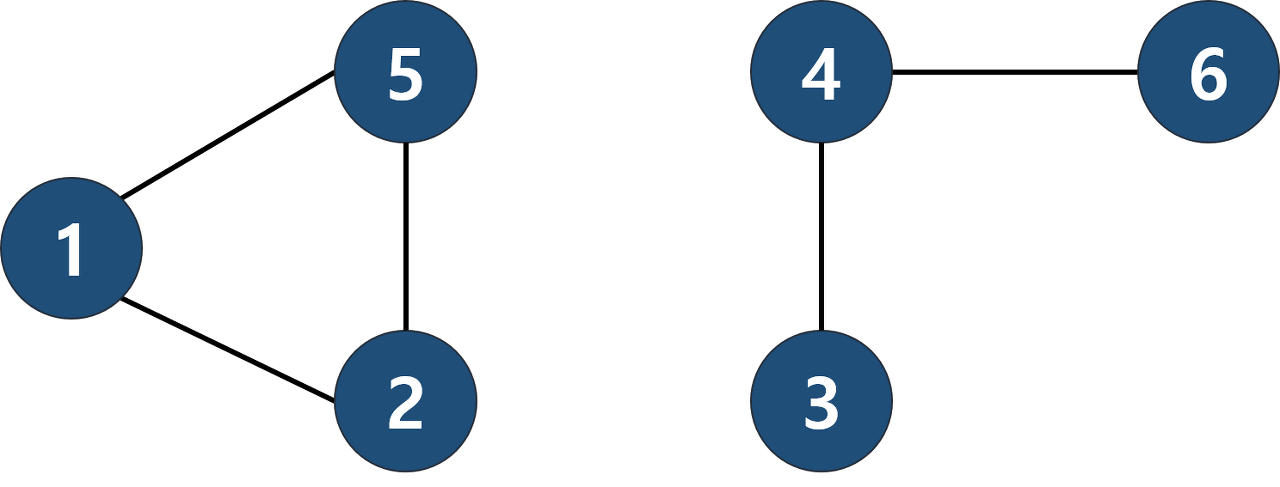
구성
- 정점 (Vertex 또는 Node)
- 간선 (Edge)
그래프의 연결 요소 Connected Component
- 서로 완전히 분리된 요소들을 '연결 요소'라고 합니다.
- 위 그림은 각각의 그래프 2개가 아닌, 연결 요소 2개로 이뤄진 그래프 1개 입니다.
그래프의 분류
1. 그래프의 방향성

| 방향 그래프 | 방향이 정해져 있음 |
| 무방향 그래프 | 어느 방향으로 가도 상관 없음 (양방향 그래프) |
2. 그래프의 순환성

| 순환 그래프 | 순환하는 부분이 한 군데만 있어도 순환 그래프 |
| 비순환 그래프 | 순환하는 부분이 전혀 없음 |
* DAG (Directed Acycilc Graph) : 방향성 비순환 그래프
* 트리 (Tree) : 무방향 비순환 그래프
※ 트리 Tree
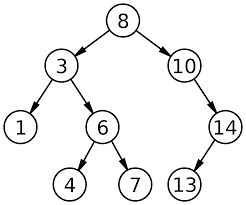
- 위와 같은 모양을 한 그래프를 '트리'라고 합니다.
- 정확히는 무방향 비순환 그래프입니다.
- 트리에서 반드시 성립하는 공식 : 노드개수 = 간선개수 + 1
그래프를 코드로 나타내기

1. 인접 행렬 Adjacency Matrix (★)
- 2차원 배열을 만들고 그 안에 값을 넣습니다.
- 정점 개수를 V라고 했을 때 시간복잡도는 O(V * V)
# False로 초기화된 인접행렬 (N + 1) * (N + 1) 크기의 adj
adj = [[False] * (N + 1) for _ in range(N + 1)]
# M개의 간선을 adj에 저장
for i in range(M):
n1, n2 = map(int, input().split())
adj[n1][n2] = adj[n2][n1] = True* 인접행렬의 크기를 (N + 1) * (N + 1)로 만든 이유 : 노드 번호가 1부터 시작하는 경우를 고려한 것입니다. (1-based)
2. 인접 리스트 Adjacency List
- 각 행이 간선의 시작 노드를 나타냅니다.
- 행마다 간선 개수만큼 각 간선의 도착 노드를 저장합니다.
- Python은 리스트로 구현합니다.
- 정점 개수를 V, 간선 개수를 E라고 했을 때 시간복잡도는 O(V + E)
그래프 탐색 알고리즘
1. DFS (깊이우선탐색, Depth First Search)

더 이상 진행할 노드가 없으면 올라와서 또 다시 다른 인접 노드로 탐색을 진행하는 방식을 DFS라고 합니다.
- 완전탐색 알고리즘
- 구현 : 스택 또는 재귀(★)
# 파이썬은 재귀호출 횟수가 1000회로 제한되어 있습니다.
# sys 모듈의 setrecursionlimit()으로 제한을 늘려줍니다.
import sys
sys.setrecursionlimit(10 ** 6)
def dfs(i):
for j in range(1, N + 1):
if adj[i][j] and not chk[j]:
chk[j] = True
dfs(j)
2. BFS (너비우선탐색, Breadth First Search)

모든 인접 노드를 탐색하고 나서 그 다음 아래 계층으로 내려가는 방식을 BFS라고 합니다.
- 완전탐색 알고리즘
- 구현 : 큐
- 최초로 목표 노드에 도달했을 때 최단거리임이 보장(★)
from collections import deque
def bfs(i):
q = deque()
q.append(i)
chk[i] = True
while q:
x = q.popleft()
for j in range(1, N + 1):
if adj[x][j] and not chk[j]:
q.append(j)
chk[j] True
3. 백트래킹

탐색 과정에서 답이 아닌 분기를 만나면 탐색을 진행하지 않고 다른 분기로 되돌아가는 방식(가지치기)을 백트래킹이라고 합니다.
- 완전탐색 알고리즘
- 기본적으로는 DFS나 BFS와 같은 방식으로 진행됩니다.
※ 길찾기 문제
설명
- DFS/BFS 단골 문제 유형
- 격자칸 형태의 board가 주어지고 위, 아래, 왼쪽, 오른쪽으로 움직이며 경로를 찾는 문제
- 아래의 코드 형태를 익혀두면 수월합니다.
- 아래 dfs와 bfs 코드 중 원하는 것을 사용하면 됩니다.
풀이법
- dy, dx에 상대 좌표를 저장해두고 다음 좌표를 구하기
- 각 격자칸의 방문 여부를 체크해두기
from collections import deque
dy = (0, 1, 0, -1)
dx = (-1, 0, 1, 0)
N = int(input())
board = [input() for _ in range(N)]
chk = [[False] * N for _ in range(N)] # 방향 그래프
# chk = [False] * N # 무방향 그래프 (이 문제는 해당사항 없음)
def is_valid_coord(y, x):
return 0 <= y < N and 0 <= x < N
def dfs(y, x):
if board[y][x] == ans:
return
for k in range(4):
ny = y + dy[k]
nx = x + dx[k]
if is_valid_coord(ny, nx) and not chk[ny][nx]:
chk[ny][nx] = True
dfs(ny, nx)
def bfs(sy, sx):
q = deque()
chk[sy][sx] = True
q.append((sy, sx))
while q:
y, x = q.popleft()
if board[y][x] == ans:
return
for k in range(4):
ny = y + dy[k]
nx = x + dx[k]
if is_valid_coord(ny, nx) and not chk[ny][nx]:
chk[ny][nx] = True
q.append((ny, nx))https://beluga9.tistory.com/370
2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
'Algorithm > 이론' 카테고리의 다른 글
| 알고리즘 유형 6. 동적 계획법 (0) | 2022.04.24 |
|---|---|
| 알고리즘 유형 5. 이분 탐색 (0) | 2022.04.24 |
| 알고리즘 유형 3. 탐욕법 (0) | 2022.04.22 |
| 알고리즘 유형 2. 완전탐색 (0) | 2022.04.22 |
| 알고리즘 유형 1. 자료구조 (파이썬) (0) | 2022.04.21 |
